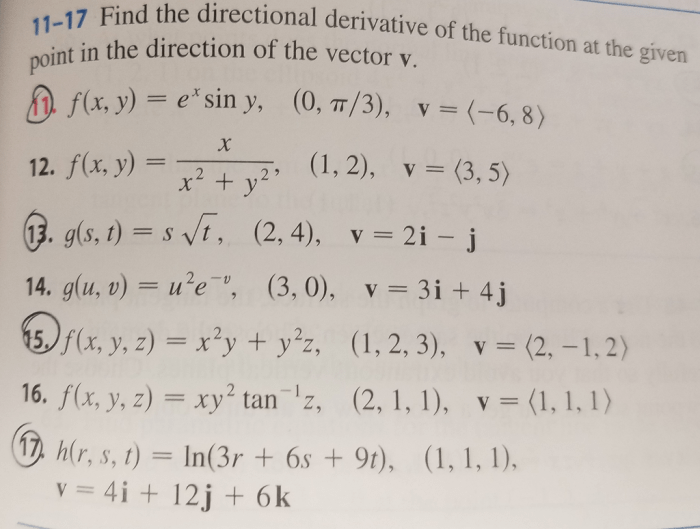Which numbers are irrational select all that apply – Embarking on an exploration of irrational numbers, this discourse delves into their intriguing nature, providing a comprehensive understanding of their properties, applications, and significance within the realm of mathematics.
Irrational numbers, characterized by their non-terminating and non-repeating decimal expansions, defy expression as fractions of integers. Their presence permeates various scientific disciplines, including geometry, physics, and beyond.
Irrational Numbers: Which Numbers Are Irrational Select All That Apply

Irrational numbers are real numbers that cannot be expressed as a fraction of two integers. They are non-terminating and non-repeating, meaning their decimal expansions never end or repeat.
Properties of Irrational Numbers
- Irrational numbers are non-terminating and non-repeating.
- Irrational numbers cannot be expressed as a fraction of two integers.
- Irrational numbers can be added, subtracted, multiplied, and divided by rational numbers.
Applications of Irrational Numbers, Which numbers are irrational select all that apply
Irrational numbers are used in a variety of real-world applications, including:
- Geometry: Irrational numbers are used to calculate the areas and volumes of circles and other geometric shapes.
- Physics: Irrational numbers are used to describe the motion of objects and the properties of materials.
- Finance: Irrational numbers are used to calculate interest rates and other financial quantities.
Irrational Numbers in Mathematics
Irrational numbers are represented in different mathematical contexts as follows:
- Algebra: Irrational numbers are represented as expressions involving square roots and other irrational numbers.
- Calculus: Irrational numbers are represented as limits of sequences and integrals.
- Number theory: Irrational numbers are studied in relation to prime numbers and other number-theoretic concepts.
Questions Often Asked
What is the difference between rational and irrational numbers?
Rational numbers can be expressed as a fraction of two integers, while irrational numbers cannot.
Can irrational numbers be approximated?
Yes, irrational numbers can be approximated to any desired degree of accuracy using decimal expansions or other methods.
Are all real numbers either rational or irrational?
Yes, every real number is either rational or irrational.